• • • • • • • Installing toolboxes and setting up the path. You need to download the and the. You need to unzip these toolboxes in your working directory, so that you have toolbox_general/ and toolbox_signal/ in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'. Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab commands you want to execute. Win64_11gr2_client Oracle. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands. Execute this line only if you are using Matlab. Getd = @(p)path(path,p);% scilab users must *not* execute this Then you can add these toolboxes to the path.% Add some directories to the path getd( 'toolbox_signal/'); getd( 'toolbox_general/'); Loading a Signal and Making Noise Here we consider a simple additive Gaussian noise. Dicionario De Acordes De Cavaquinho Em Pdf.

This MATLAB function returns the horizontal (vertical or diagonal, respectively) coefficients obtained from the wavelet decomposition structure [C,S] (see wavedec2.

First we load the 1D signal.% size n = 2048;% clean signal name = 'piece-regular'; x0 = load_signal(name, n); x0 = rescale(x0.05.95); Then we add some Gaussian noise. Sigma = 0.07; x = x0 + randn(size(x0))*sigma; Display. Clf; subplot(2,1,1); plot(x0); axis([1 n 0 1]); title( 'Clean signal'); subplot(2,1,2); plot(x); axis([1 n 0 1]); title( 'Noisy signal'); Hard Thresholding vs. Soft Thresholding A thresholding is a 1D non-linear function applied to each wavelet coefficients. • First one must use a lower threshold because soft thresholding also lower the value of non-thresholded coeffcients.

In practice, a threshold of 3/2*sigma works well. • The low frequency part of the coefficients must not be thresholded. T = 1.5*sigma; xWT = perform_thresholding(xW,T, 'soft');% re-inject the low frequencies xWT(1:2^Jmin) = xW(1:2^Jmin);% re-construct xsoft = perform_wavelet_transf(xWT,Jmin,-1,options); We can display the results.

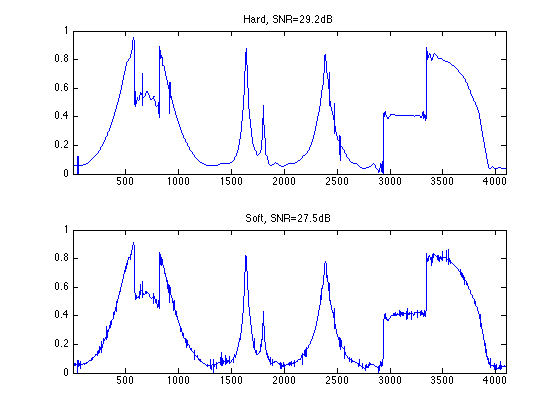
Clf; subplot(2,1,1); plot(xhard); axis([1 n 0 1]); title(strcat([ 'Hard denoising, SNR=' num2str(snr(x0,xhard))])); subplot(2,1,2); plot(xsoft); axis([1 n 0 1]); title(strcat([ 'Soft denoising, SNR=' num2str(snr(x0,xsoft))])); Exercice 1: (the solution is ) Determine the best threshold T for both hard and soft thresholding. Test several T values in [.8*sigma, 4.5*sigma]. Do not forget to keep the low frequency wavelet coefficients. What can you conclude from these results? Test with another image. Exo1; Translation Invariant Wavelet Transform Orthogonal wavelet transforms are not translation invariant. It means that the processing of an image and of a translated version of the image give different results.

A translation invariant wavelet transform is implemented by ommitting the sub-sampling at each stage of the transform. Maslanka Traveler Program Notes. This correspond to the decomposition of the image in a redundant familly of N*(J+1) atoms where N is the number of pixel and J is the number of scales of the transforms. For Scilab, we need to extend a little the available memory.

Extend_stack_size(4); The invariant transform is obtained using the same function, by activating the switch options.ti=1. Options.ti = 1; xW = perform_wavelet_transf(x0,Jmin,+1,options); xW(:,:,1) corresponds to the low scale residual. Each xW(:,1,j) corresponds to a scale of wavelet coefficient, and has the same size as the original signal. NJ = size(xW,3); clf; subplot(5,1, 1); plot(x0); axis( 'tight'); title( 'Signal'); i = 0; for j=1:3 i = i+1; subplot(5,1,i+1); plot(xW(:,1,nJ-i+1)); axis( 'tight'); title(strcat([ 'Scale=' num2str(j)])); end subplot(5,1, 5); plot(xW(:,1,1)); axis( 'tight'); title( 'Low scale'); Translation Invariant Wavelet Denoising Orthogonal wavelet denoising does not performs very well because of its lack of translation invariance.

A much better result is obtained by not sub-sampling the wavelet transform, which leads to a redundant tight-frame. First we compute the translation invariant wavelet transform options.ti = 1; xW = perform_wavelet_transf(x,Jmin,+1,options); Then we threshold the set of coefficients. T = 3.5*sigma; xWT = perform_thresholding(xW,T, 'hard'); We can display some wavelets coefficients J = size(xW,3)-2; clf; subplot(2,1,1); imageplot(xW(:,:,J)); title( 'Noisy coefficients'); subplot(2,1,2); imageplot(xWT(:,:,J)); title( 'Thresholded coefficients'); We can now reconstruct. Xti = perform_wavelet_transf(xWT,Jmin,-1,options); Display the results. Clf; subplot(2,1,1); plot(xhard); axis([1 n 0 1]); title(strcat([ 'Hard orthogonal, SNR=' num2str(snr(x0,xhard))])); subplot(2,1,2); plot(xti); axis([1 n 0 1]); title(strcat([ 'Hard invariant, SNR=' num2str(snr(x0,xti))])); Exercice 2: (the solution is ) Determine the best threshold T for both hard and soft thresholding, but now in the translation invariant case.